Den filosofiske matematikbog – Euklids Elementer

Et af de mest markante aftryk, antikken har sat på vores verden i dag, er gennem matematikken. Og det kan vi takke Euklid og hans værk Elementer for. Cand.mag Chr. Gorm Tortzen forklarer, hvordan Euklid banede vejen for, at vi som samfund i dag accepterer, at verden med fordel kan beskrives i tal og linjer.
Den antikke verden har efterladt sig mange og meget forskelligartede spor: Bygninger, kunstværker og mange former for litteratur, som på forskellige tidspunkter i den senere historie har sat sig dybe og ofte meget synlige spor. I Danmark har man på adskillige museer direkte adgang til antikkens kunstværker, overalt er der i den ældre bygningsmasse arkitektoniske citater fra oldtidens bygningsværker, og der udgives jævnligt nye oversættelser af Homers Iliade, Sofokles’ Ødipus, Platons dialoger og mange andre klassikere. Én side af den antikke arv kommer sjældnere frem i lyset, selvom den nok har sat sig endnu dybere spor: matematikken og de eksakte videnskaber. I fysikken, geografien, biologien og medicinen har man for længst distanceret sig fra antikkens forskning, selvom man er helt afhængig af dens terminologi; derimod står ét værk uantastet som fundamentet for matematikken: Euklids Elementer, der netop er udkommet i en ny dansk oversættelse.
Mange af Euklids beviser bruges stadig i skoleundervisningen – tænk bare på den såkaldte pythagoræiske læresætning, som alle kan sige i en simplificeret form: ’a i anden plus b i anden er lige med c i anden’ – som regel uden at kunne føre beviset. Andre af de over 600 sætninger lever en mere stille tilværelse. Jeg vil i det følgende prøve at vise, hvorfor Euklids bog ikke blot er et interessant matematikhistorisk værk, men faktisk er endnu en nøgle til at forstå antikkens store filosofiske skoler og deres interesse for vekselvirkningen mellem det synlige og foranderlige, fænomenverdenen, og den evige, uforanderlige verden, som Platon og især eftertiden kaldte idéverdenen.
En Euklid-biografi
Navnet Euklid er i de flestes ører nok synonymt med geometri. Det er for så vidt også rigtigt, for hans mest kendte værk er uden diskussion Elementer i 13 bøger, et skelsættende værk i historien og med en meget lang virkningshistorie, som jeg vil vende tilbage til.
Euklids biografi er hurtigt overstået: Hans græske navn er det temmelig almindelige Eukleides, ’den der har et godt ry’, han var aktiv i den nye storby Alexandria omkring 300 f.Kr., det vil sige kort efter byens grundlæggelse. Alexander den Store havde selv givet navn til byen, og efter hans død herskede hans general Ptolemaios enevældigt over den sammen med det egentlige Ægypten. Grækerne opbyggede på meget kort tid en helt ny metropol på Afrikas nordkyst, og hertil strømmede mange intellektuelle fra alle dele af den græske verden. Euklid meddeler intet som helst om sig selv, og vi kan derfor kun slutte os indirekte til hans herkomst, uddannelse og formålet med hans Elementer. Værket afslører dog så meget om hans videnskabelige og filosofiske ståsted, at det er rimeligt at antage, at han var uddannet i Athen, som i et århundrede havde været centrum for videnskaben med frontfigurerne Sokrates, Platon, Aristoteles og Eudoxos. Alexandria gjorde med andre ord det samme som de amerikanske universiteter efter krigen: De ptolemæiske konger støvsugede landskabet for videnskabeligt potentiale i det gamle land og opbyggede på kort tid en forskningsinstitution, Museion, som på mange måder overgik de gamle skoler i Athen, først og fremmest Platons Akademi og Aristoteles’ Lykeion. Alt tyder på, at den unge Euklid er fulgt med strømmen, og at han i det nye Alexandria har fået muligheder for at udvikle sit mageløse værk i et aktivt videnskabeligt miljø, der senere talte stjerner som Archimedes, der bestemte legemers opdrift i væske, formulerede vægtstangsreglen og den approximerede værdi af π, og Eratosthenes, som med et genialt geometrisk ræsonnement målte Jordens omkreds. Det var samme Eratosthenes, der som den første kunne ’si’ primtallene ud af den uendelige talrække, hvilket stadig har betydning, når man skal konstruere koder eller bitcoins.
Hvor i Athen Euklid er blevet uddannet og af hvem, kan man kun gætte på, men hans matematiske begrebsverden og det medfølgende sprog peger på en af de gamle skoler.
Elementerne
Elementerne er som sagt på 13 ’bøger’, der for nogles vedkommende passer nogenlunde med en bogrulle, mens andre langt overskrider kapaciteten på en papyrusrulle, der rummer ca. 35-40 af vores tryksider. Man har i spøg sagt, at Elementerne er den eneste græske bog, der ikke kræver forudviden om græsk mytologi og historie, og det er for så vidt sandt – derimod får man et langt større udbytte af den, hvis man ved lidt om den filosofiske og matematiske forudsætning, som den uden videre går ud fra. Der er nemlig ingen indledning, ingen forklaring på forudsætninger og målsætning, kun en lige-på-og-hårdt-tekst, der uden nærmere forklaring begynder med: ’Et punkt er det, som ikke har nogen del’. Det bliver man jo ikke så meget klogere af, medmindre man har en lærer ved hånden, der kan forklare mål og med i dette forunderlige værk.
Inden vi går videre, er det klogt at få slået fast, hvad Elementer betyder. Ordet er latin og er en oversættelse af det græske Stoicheia, der i sin grundbetydning har ’gå, stå, være i række og geled’. I aflydsformen stich- bruges det om en verselinje (stichos), Stoichaderne er en række øer i Ægæerhavet, som ligger som på en snor, stoichos er et geled soldater eller sten i et murværk, stoicheion er viseren på et solur, der marcherer taktfast over skiven, og det betyder derfor også ’mindste element i en større sammenhæng’ – ligesom dets latinske oversættelse Elementum. Der findes ligefrem et verbum, der betyder ’opstiller i en ordnet rækkefølge’ stoicheióo, og Euklid selv får i den senere antikke kommentarlitteratur ærestitlen Stoicheiótes ’den der opstiller elementerne’ eller måske bedre: Systembyggeren. Elementer betyder altså et system opbygget som et korthus, hvor hver enkeltdel er placeret på sin rette plads og er forudsætningen for det videre systematiske bygningsarbejde, indtil slutmålet er opnået.
For et system er det. Fra den første definition af ’punkt’ til sidste sætning i 13. bog går der en lige linje, hvor element bliver lagt på element. Alle elementer er enten definitioner (for eksempel hvad en linje er, en cirkel, en diameter, en trekant og så videre) postulater (for eksempel alle rette vinkler er lig med hinanden), aksiomer (det berømteste er: ’De størrelser, som er lig men en og samme størrelse, er også lig med hinanden’), eller også er de resultatet af et bevis. Det er langt de fleste. Metoden kaldes aksiomatisk, og Euklids Elementer er det ældste eksempel på denne fremgangsmåde, som har sat sig helt afgørende spor i videnskaben over hele verden, ikke blot i Vesten.
Værket er disponeret i fire hovedafdelinger: Bøgerne I-VI handler om plangeometri, VII-IX om talteori og forholdslæren, X (der er lige så lang som tre af de andre bøger tilsammen) om kommensurable linjestykker og rektangler, og endelig XI-XIII om rumgeometri. I det følgende vil jeg stort set kun beskæftige mig med de seks første bøger, som netop er blevet oversat til dansk. Disse seks bøger er så langt de allerfleste når i geometri, og de er derfor også dem, der har fået den største virkningshistorie.
Proklos om Euklids værker
Den senantikke filosof Proklos (400-tallet e.Kr.) har skrevet en oversigt over geometriens historie og omtaler her Euklid og hans værk med disse ord:
“… Af overbevisning er han platoniker og fortrolig med denne filosofi, og derfor sætter han også slutstenen på Elementerne med konstruktionen af de såkaldte platoniske legemer. Hans mange andre matematiske værker er fulde af en beundringsværdig præcision og videnskabelig indsigt. Sådan er nemlig hans Optik og Lære om Spejle, sådan er hans Elementer i Musikken og hans lille bog Om Opdelinger.
Man må dog i særlig grad beundre ham for hans Elementer i Geometrien på grund af deres organisering og valg af sætninger og konstruktioner med sigte på den ordnede opstilling. Men mange ting kan tilsyneladende stemme overens med sandheden og være en følge af de videnskabelige principper, mens de i virkeligheden fører til en afvigelse fra udgangspunktet og narrer de mere overfladiske; derfor har han også givet os metoder til en gennemskuende forståelse af den slags, og når vi har dem, kan vi træne begynderne i at afsløre falske argumenter og derved undgå at blive ledt på vildspor. Dette værk, hvori han har givet os dette redskab, har han givet navnet Falske Konklusioner… Denne bog renser og træner, mens Elementerne omfatter en uigendrivelig og fuldkommen gennemgang af den videnskabelige teori om emner inden for geometrien. For han tog ikke alt det med, som han havde til sin rådighed, kun hvad han kunne stille op i rækkefølge. Han inddrog også alle former for syllogismer, både dem der henter deres troværdighed fra årsager, og dem der tager udgangspunkt i beviser…”
Man må nok tage forbehold over for nogle af Proklos’ påstande. Det er givet, at Euklid ikke kunne være platoniker på samme måde som nyplatonikeren Proklos var det 700 år senere – og som han meget forståeligt gerne ville have sit idol til også at være. At man slutter sit værk med konstruktionen af de fem regulære polyedre er ikke ensbetydende med, at man skriver under på alle Platons teorier om sjælevandring, generindring, det gode samfund og så videre, men Proklos’ beskrivelse af Elementerne som et avanceret og stringent sammenhængende aksiomatisk værk opbygget af tidligere græske matematikeres arbejde er fuldt dækkende. Der er dog ingen tvivl om, at geometrien spillede en stor rolle i undervisningen i Platons Akademi og Aristoteles’ Lykeion. Det viser adskillige eksempler fra deres værker meget tydeligt, og her fremgår det også, at geometrien lærer mennesket meget mere end bare at tegne trekanter og desuden er uundværlig for arkitekter og håndværkere. Jeg vil nedenfor give eksempler på Platons opfattelse af geometrien som erkendelsesredskab, men først skal bogen og dens metode præsenteres.
Euklids metode
Vil man se nærmere på Euklids metode, må man forstå hans tredobbelte fremgangsmåde. Som nævnt går han uden nærmere begrundelse ud fra nogle ubeviselige definitioner – og hvis man ikke vil acceptere dem, slutter legen her, ganske svarende til reaktionen, hvis man ikke vil anerkende, at et kortspil består af 52 kort i fire farver, og at spillereglerne for for eksempel hjerterfri er sådan og sådan. Men gør man det, altså accepterer Euklids definitioner, postulater og aksiomer, går vejen gennem sætninger, der fordeler sig i beviser (theoremer), som netop beviser, at noget under visse forudsætninger er tilfældet, og i konstruktioner (problemer), som påviser, at et eller andet rent faktisk kan lade sig gøre. Lad os tage det sidste først:
Første sætning i Første Bog er en konstruktionsopgave:
Bog I.1
At konstruere en ligesidet trekant på en given begrænset ret linje.
[Vi har altså uden nærmere forklaring end definitionerne en given begrænset linje, og på den skal vi (igen uden en egentlig forklaring) konstruere en ligesidet trekant. Euklid bestemmer! Så følger sætningen slag i slag:]
Lad AB være den givne begrænsede rette linje. Der skal nu konstrueres en ligesidet trekant på den
rette linje AB.
★
[Stjernen betyder, at nu skal læseren arbejde og tænke med; henvisningerne i […] dokumenterer, at den pågældende ’handling’ er tilladt ifølge spillereglerne. P = Postulat, D = Definition]
Lad cirkel BCD være tegnet med A som centrum og AB som radius [P3], og endvidere cirkel ACE
med B som centrum og BA som radius, og lad de rette linjer CA og CB være trukket fra punkt C,
hvor cirklerne skærer hinanden, til punkterne A og B [P1].
Da punkt A er centrum i cirkel CDB, er AC lig med AB [I.D15]; da endvidere punkt B er centrum
i cirkel CAE, er BC lig med BA. Og det blev også bevist, at CA er lig med AB; både CA og CB er
altså lig med AB. Men de størrelser, som er lig med samme størrelse, er lig med hinanden [A1].
Altså er CA lig med CB. De tre linjer CA, AB og BC er altså lige store.
Altså er trekant ABC ligesidet [I.D20]. Og den er konstrueret på den givne begrænsede rette linje AB.
Hvilket skulle gøres.
Denne tekst er en præcis gengivelse af den græske, men de fleste vil vist være enige i, at den er stort set uforståelig. Det skyldes, at den endnu ikke er ledsaget af en forklarende figur:
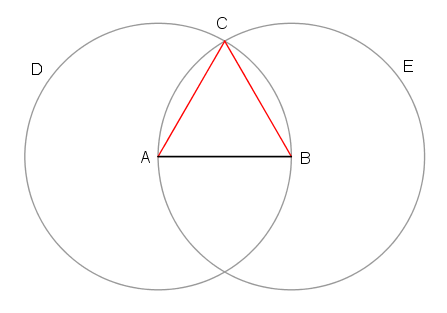
Herefter bliver alt klart – særligt hvis man selv tegner med – og teksten står soleklar for en (hvorfor havde jeg ikke tænkt på det selv? spørger man sig). Det er også klart, at Euklid og alle antikke geometrer benyttede sig af figurer, ja det er højst sandsynligt, at figurerne i virkeligheden er det bærende i hele fremstillingen, og at det er dem, studenterne skulle indprente sig og lære udenad. Teksten kan selvfølgelig ikke undværes, men tilsammen udgør de det nødvendige hele. Måske skulle man tilføje, at læserens medtegning af figuren udgør den endelige nøgle til forståelsen. Men det siger Euklid ikke noget om.
Her er vi ved noget meget centralt ved Euklids måde at fremstille problemer og deres løsning på: Han optræder som en slags tryllekunstner, der for det forbløffede publikum fremtryller løsninger uden rigtig selv at være til stede i lokalet. Bemærk, at alle ordrer gives til en ukendt person. På græsk bruges en sær verbalform, kaldet perfektiv imperativ 3. person, som nærmest ud i luften beordrer, at noget allerede skal være udført af en person, som i øvrigt ikke nævnes. Vi oversættere har givet ham kælenavnet Den Hjælpende Hånd. Han er en slags pedel, som gør det praktiske arbejde på tavlen, mens professoren ser til i ophøjet ro. Den Hjælpende Hånd har passer og lineal til sin rådighed, men det er alt sammen kun til ære for den uvidende hob, for ingen af tegningerne er andet end tydeliggørelser, eksemplificeringer på tavlen af kendsgerninger, som er uafhængige af, om vi har fattet dem eller ej. Euklid er på en måde ligeglad, om vi forstår argumentationen; det er vores problem. Hans interesse ligger i at lave modsigelsesfrie beviser og konstruktioner. Han er givetvis også ligeglad med geometriens praktiske anvendelse. Elementerne er ikke et pædagogisk værk, Euklid er ikke pædagog – tværtimod er han kun interesseret i at skrive et geometrisk manifest rettet til ligemænd, ikke til skoleelever. Dette har han allerede gjort i den ovenfor nævnte bog Falske Konklusioner, der desværre ikke har overlevet. Den popularitet, som Elementerne opnåede i det vestlige skolevæsen, hviler altså på en måde på et falsk grundlag. Bogen er ikke skrevet til børn.
Noget andet er så, at bogen (især de seks første bøger) udmærket kan bruges og stadig bliver brugt som introduktion til den todimensionale geometri, plangeometrien. Men det kræver lidt pædagogisk knofedt at gøre det interessant og vedkommende, og det er ikke altid lykkedes ude i trummerummen ved tavlen.
Euklids bog
Ved et lykketræf fandt man i 1898 i Ægypten en stump af en papyrus fra 75-125 e.Kr., altså 400 år efter Euklid. Stumpen indeholder lidt af sætning II.5 (et bevis) og en figur. Linje 2 begynder med et vanskeligt genkendeligt E (= 5) og fortsætter – uden ordmellemrum: ΕΑΝ ΕΥΘΕΙΑ ΓΡΑΜΜ… ΤΜΗΘΗ ΕΙΣ ΙΣΑ ΚΑΙ… det vil sige: Hvis en ret linje deles i lige store og … Sammenlign tegningen med oversættelsens nedenfor. Papyrusskriveren har ikke angivet bogstaverne, men ellers er tegningerne ganske ens – ligesom i hele håndskrifttraditionen. Euklid bruger kun store bogstaver – de små blev først indført i 800-tallet e.Kr.

Prøv derefter med papir og blyant ved hånden at læse sætningen:
Bog II.5
Hvis en ret linje deles i lige store og i ulige store stykker, er det rektangel, der indesluttes af hele linjens ulige store stykker plus kvadratet på stykket mellem delingspunkterne, lig med kvadratet på halvdelen.
Lad nemlig en ret linje AB være delt i lige store stykker i C og i ulige store stykker i D. Jeg påstår, at det rektangel, der indesluttes af AD og DB plus kvadratet på CD, er lig med kvadratet på CB.
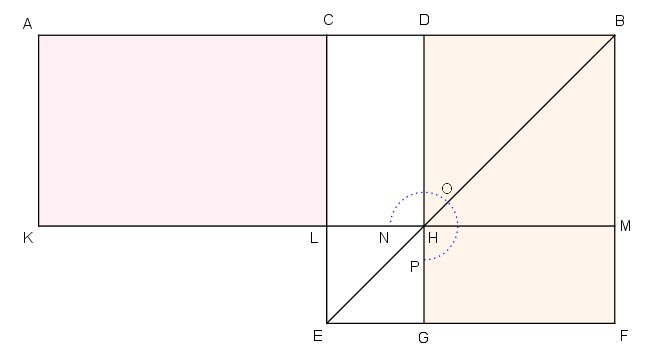
★
Lad der nemlig på CB være tegnet kvadratet CEFB [I.46]; lad BE være trukket, lad DG være trukket gennem D parallelt med CE eller BF, lad KM være trukket gennem H parallelt med AB eller EF, og lad endelig AK være trukket gennem A parallelt med CL eller BM [I.30, I.31]. Da udfyldningsfigur CH er lig med udfyldningsfigur HF [I.43], skal DM være lagt til dem begge; altså er hele CM lig med hele DF [A.2]. Men CM er lig med AL, fordi AC er lig med CB [I.36]. Altså er AL lig med DF. Lad CH være lagt til dem begge, så er hele AH lig med gnomon NOP. Men AH er rektanglet indesluttet af AD og DB; for DH er lig med DB, altså er gnomon NOP lig med det, der er indesluttet af AD og DB. Lad LG, som er lig med kvadratet på CD, være lagt til dem begge; så er gnomon NOP plus LG lig med rektanglet indesluttet af AD og DB plus kvadratet på CD. Men gnomon NOP plus LG er hele kvadratet CEFB, som er kvadratet på CB. Altså er rektanglet indesluttet af AD og DB sammen med kvadratet på CD lig med kvadratet på CB.
Altså: Hvis en ret linje deles i lige store og i ulige store stykker, er det rektangel, der indesluttes af hele linjens ulige store stykker plus kvadratet på stykket mellem delingspunkterne, lig med kvadratet på halvdelen. Hvilket skulle bevises.
Elegant, ikke?
Euklid og Platon
Det er ganske interessant, at Platon, der jo er to-tre generationer ældre end Euklid (Platon levede i årene 427-347 f.Kr.), i sine skrifter tydeligt viser, at Euklids matematik var velkendt stof i dannede kredse i Athen, og at han selv både beherskede geometrien og opfattede den som afgørende for et ungt menneskes udvikling og dannelse. I dialogen Menon hjælper Platons alter ego, Sokrates, en slavedreng til at føre bevis for, at arealet af et kvadrat fordobles, hvis man tager diagonalen som udgangspunkt for det nye kvadrat. Sokrates bruger det som argument for, at slaven i egenskab af menneske har al viden skjult i sin udødelige sjæl, og at den kun venter på at blive vækket eller ’generindret’.
I Staten gør Sokrates ligefrem geometrien til et af de grundlæggende fag i uddannelsen af samfundets støtter, de såkaldte vagter eller vogtere. Faget gør sammen med aritmetik, musik og astronomi folk til bedre mennesker og bedre samfundsborgere i det nye idealsamfund. Grunden er, at mennesket har potentialer, som både er positive og negative, og i det nye samfund skal de nyttige anlæg udvikles (og de destruktive fjernes eller minimeres). Vagternes opgave er at regulere samfundet efter ’lov-og-orden-principper’ udstukket af de langt klogere ledere, filosofferne. Vagterne skal derfor opdrages til at parere ordre, og deres aggression skal tæmmes, samtidig med at deres fysik skal være i topform. Det sidste sørger gymnastikken for, mens matematikken, astronomien og musikken gør dem til harmoniske mennesker ved at udvikle deres intellekt – eller psyche, som Platon siger. Man øjner i disse tanker konturerne af det moderne almene gymnasium.
Selvom Euklid som sagt ikke kan tages til indtægt for hele Platons mangeartede tankesæt, kan et af hans allerstærkeste billeder, hulebilledet fra Statens syvende bog, godt bruges til at illustrere, hvordan han opfatter geometrien – og der er næppe tvivl om, at Euklid ville skrive under på billedet også.
Hulebilledet
Platon lader Sokrates fortælle følgende historie: Du skal tænke dig en dyb hule. Helt nede i bunden af den ligger der nogle fanger, som er lænket, så de ikke kan dreje hovedet, men kun se mod hulens bagvæg. Bag dem, altså længere oppe i hulen, er der et bål, og mellem bålet og fangerne er der en vej. Når nogen går på vejen, ser fangerne derfor kun skyggerne af de forbipasserende – ligesom dukkerne i et skyggeteater. Fangerne kan også høre de forvrængede stemmer, men da de jo ikke ved bedre, må de opfatte dette som virkeligheden. Dette er deres verden, og her føler de sig hjemme og konkurrerer indbyrdes om magt og ære. Nu er der imidlertid en af fangerne, som får løsnet lænkerne og kan dreje hovedet – med det resultat, at han bliver blændet af bålets flammeskær. Han vil helst vende sig igen til det trygge og hjemlige, men bliver forhindret af en person, der senere også tvinger ham til at rejse sig og gå forbi bålet og op til hulens munding, hvor der er endnu stærkere lys – både dag og nat. Først langsomt og modvilligt lader fangen sig overbevise om, at der er en mere virkelig virkelighed uden for hulen, hvor det rigtige lys, sollyset skinner. Solen er den ultimative lyskilde, og lys giver menneskets iboende synssans mulighed for at virke og få indsigt. Når ex-fangen vender hjem til hulens mørke, er han mørkeblind, han falder over sine ben og bliver til grin blandt huleboerne, der sagtens kan finde ud af det i mørket. Faktisk ønsker de fleste af dem, der kommer op i lyset, ikke at vende tilbage, fordi de ved, at de bliver udsat for chikane og ringeagt, når de fortæller huleboerne, at der er en rigtig verden uden for deres skyggeverden, som kun er en afglans af virkeligheden. Derfor vender kun få tilbage, mens resten bare er glade for at være sluppet ud og væk.
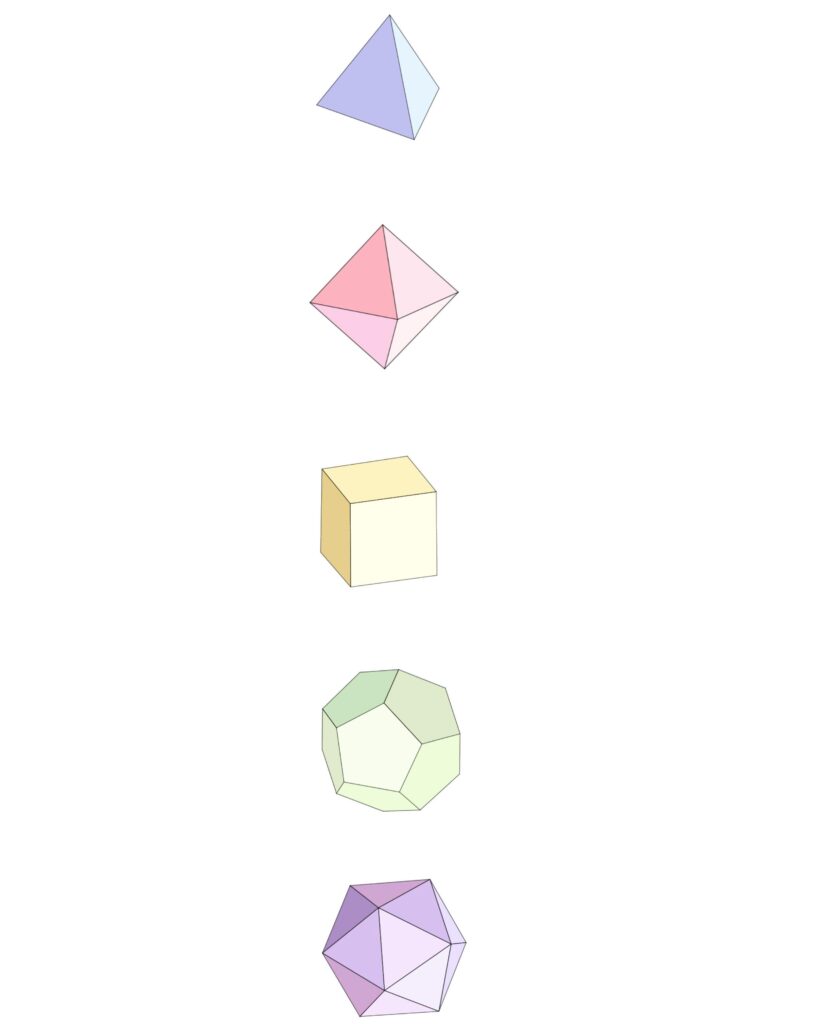
Platons hulebillede kan bruges (og misbruges) til mange ting, men i geometrisammenhæng kan billedet illustrere, hvad der sker under et bevis: Euklid begynder oppe i det abstrakte, forstandens klare lys. Derefter bevæger han sig ned i hulen – til tavlen på bagvæggen, hvor Den Hjælpende Hånd tegner linjer og slår cirkler, som egentlig er ganske ligegyldige, fordi de allerede eksisterer oppe i virkeligheden. De har kun ét formål: At forklare fangerne, det vil sige læserne, hvordan virkeligheden ser ud ovenfor. Når vi tegner med, får vi i ét berusende nu indsigt i, hvordan virkeligheden udenfor ser ud. Og geometrien er virkeligheden. Derfor er det, at Platon i dialogen Timaios lader den pythagoræiske filosof af samme navn forklare, at kosmos i virkeligheden består af de fem regulære polyedre, som Euklid ender med at konstruere i 13. bog – hvorefter han viser, at der er disse fem, hverken flere eller færre.
Euklids sprog
Når man arbejder med Euklid – særligt når man oversætter ham til et så fjernt sprog som dansk – bliver man opmærksom på en række ejendommelige forhold. For det første har Euklid ikke som vi to oldtidssprog at hente gloser i. Vi kan for eksempel frit plukke i græsk og latin, når vi skal lave et nyt ord for et eller andet: Dino-saurus betyder:’farlig øgle’, tele-vision: ’fjern-syn’ grammo-fon: ’streg-lyd’ (fordi lyden gemmes i rillen på pladen), inter-national: ’mellem-folkelig’ og så videre og så videre. Han havde kun det græske dagligsprog og den geometriske praksis at gå ud fra. Ordet geo-metri er mønstereksemplet: ’Jord-måling’ var nok oprindelig et meget godt ord for opmåling af agerjord, men på Euklids tid var det kommet til at betyde noget ganske andet og mere abstrakt. Overvej som tankeeksperiment, hvordan vores naturvidenskabelige terminologi ville se ud uden græsk og latin! Euklid og hans kolleger gjorde selvfølgelig det eneste rigtige: De udvalgte dagligdags ord og definerede dem til entydige størrelser: ’En linje er en længde uden bredde’ [D2]. Linje er en oversættelse af gramme, der egentlig betyder ’noget tegnet, en streg’, ligesom punkt, semeion egentlig betyder ’mærke’ og centrum ’prik’, nemlig i midten af cirklen. I vores oversættelse er den latinske oversættelse af Euklid smuglet ind: Linje er et lån fra linea, punkt fra punctum, cirkel fra circulus, rektangel fra rectangulum ’ligehjørnet’ og så videre.
Et andet overraskende træk er de meget få fagtermer, som Euklid benytter sig af. Nogle er defineret – det gælder substantiver (punkt, linje, trekant, diagonal) og adjektiver (lige, ulige, ligedannet, ret, stump), der alle betegner tilstande eller egenskaber ved de evige figurer ’oven over hulen’, mens transaktionerne nede på hulevæggen, der selvfølgelig udtrykkes i verber, ikke defineres. De er jo heller ikke nødvendige i samme grad, fordi handlingerne/konstruktionerne kun foregår på hulens tavle og af Den Hjælpende Hånd. Faktisk kan Euklid klare sig med ca. 200 ord i de første seks bøger, herunder en mængde ’transaktionsord’ (for eksempel afsætter, tegner, fratrækker, oprejser), som han ikke definerer.
Sproget er monotont, og det er med vilje, for når et ord én gang har fået sin betydning i det geometriske univers, er det uhensigtsmæssigt at bruge andre synonymer, som man ville gøre, hvis man skrev en skønlitterær tekst. Jeg har ikke tal på, hvor mange gange Euklid bruger ordet ara ’altså’ som indledning til en konklusion – men det skal naturligvis i oversættelsen klart fremgå, at der står ara hver gang, ligesom ’kvadrat’ og ’firkant’ ikke bare kan bytte plads, som det kan i daglig tale. Euklids sprog er en form for formelsprog, men uden den moderne matematiks symboler, og det er efter vores, oversætternes, mening vigtigt, at den moderne læser forstår og påskønner dette særtræk ved Euklids stil, som i øvrigt er gået i arv til mange videnskaber.
Hvorfor en ny oversættelse?
Euklid har været oversat tre gange før til dansk: I 1744 (Ziegenbalg), 1803 (Linderup) og 1897-1912 (Thyra Eibe). Thyra Eibes gode oversættelse er den første, som benytter en videnskabelig tekstudgave som grundlag, men den mangler af gode grunde en række ting, som de sidste godt hundrede års Euklidforskning har gjort mere og mere tydeligt. Hun var – som alle andre – et barn af sin tid og særligt af den danske matematikprofessor H.G. Zeuthen, der docerede, at den græske matematik bedst kunne forstås, hvis den ’oversattes’ til moderne nomenklatur. Hendes lærer var den store filolog J.L. Heiberg, som stod for den videnskabelige udgave af Euklid (1886), der den dag i dag er standardreferencen. Han forsynede sin tekst med en latinsk oversættelse (for at matematikerne lettere kunne følge med), og i den indførte han alskens symboler, som går igen i Thyra Eibes noget altmodische danske gengivelse. Hendes bog var beregnet på at være en lærebog i geometri, og den er fuldstændig blottet for indledning, noter eller andre forklaringer – altså ligesom forlægget.
Vi har i vores (fjerde danske) oversættelse haft en helt anden tilgang svarende til nutidens opfattelse af græsk naturvidenskab, nemlig at teksterne skal forstås i deres sammenhæng med den øvrige videnskabelige og filosofiske litteratur. Derfor fylder vores bog meget mere end Eibes, men vi bilder os ind, at vi er bedre ambassadører for Euklids egentlige ærinde: at læseren selv skal forstå, hvordan den virkelige verden uden for hulen ser ud, og hvordan man kan erkende det.
Euklids rolle
Euklid står på skuldrene af en lang række græske matematikere, som vi af mangel af bedre kalder pythagoræerne, og for hvem det var indlysende, at der er to verdener: Den foranderlige fysiske verden, som vi selv er en del af, og en uforanderlig, ikke-fysisk verden, hvor geometrien og aritmetikken befinder sig. Hans aksiomatiske fremstilling blev toneangivende for forskere som Archimedes og med ham renæssancens matematikere og filosoffer, og Euklids rolle som systemopbygger kom til at spille en helt afgørende rolle for naturvidenskaben også i nyere tid.
Tænk, hvis denne tanke om forbindelsen mellem det foranderlige og det evige ikke havde slået rod i den antikke og senere naturvidenskab. Hvor ville ingeniørkunsten, it-boomet, fysikken og kemien være, hvis vi ikke accepterede, at verden kan beskrives i tal og linjer? Hvis antikken er til stede i det moderne samfund, så er det nok allermest i naturvidenskaben.
Chr. Gorm Tortzen er cand.mag i klassisk filologi og lektor emeritus ved Helsingør Gymnasium og Københavns Universitet. Han har sammen med Claus Glunk, Hanne Eggert Strand og Chr. Marinus Taisbak oversat og introduceret Euklids første seks bøger om plangeometrien, som udkom i foråret 2021 på Gyldendal. Oversættelsen af de resterende bøger forventes at udkomme i 2022.


